The late Theos Thompson, a commissioner in the Atomic Energy Commission, gave a talk in November 1970 to the plasma physics division of the American Physical Society entitled “Fusion Power—the Uncertain Certainty.” Characteristically, in picking that title Tommy Thompson put his finger on the key feature of the topic he was to discuss. I feel that I could do no better in adopting his phrase as a theme.

Fusion power does not exist today. What exists is a well-grounded worldwide research effort specifically aimed toward achieving it, plus recent evidence that says this research effort is on the right track. There is growing acceptance of the proposition that power from fusion not only will be achieved but that fusion offers an almost ideal answer to our future energy needs. Fusion will be and needs to be achieved, that is the certainty. But there is also a feeling on the part of many that not only is fusion a highly desirable goal, but that it is not necessarily a distant one—if we move now. Fusion Power: Is it a distant dream or a near-term possibility? That is the uncertainty.

Controlled fusion research began about 20 years ago, in secrecy and essentially simultaneously in the United States, the United Kingdom, and the USSR. Secrecy was ended by international agreement in 1958, and since that date an unusually high degree of international cooperation has existed in this field. The present worldwide fusion effort amounts to about $120 million equivalent—about 50 percent in the Soviet Union, 25 percent in the United States (that is, about $30 million per year), and the rest in the United Kingdom, Western Europe and Japan.

Before getting to details, I’ll review some fusion basics. Fusion research seeks ways to extract useful power from nuclear reactions among light elements. The primary fuel for fusion is deuterium, heavy hydrogen. Deuterium exists in sufficient quantity to satisfy any conceivable energy demands for thousands of millions of years. The cost of obtaining it by isotope separation from water is so low that as a fuel deuterium would cost less than one percent of the present cost of coal, on a per­unit-of-energy basis.

Nuclear fusion is nuclear combustion, the process that heats the sun and the stars. To achieve controlled fusion on Earth, we must carry out the following steps: First, heat a small quantity (how small I will mention later) of fusion fuel above its ignition point—about 100 million degrees kinetic temperature. Second, maintain this fuel in a heated condition long enough for the release of fusion energy to exceed the heat input, and third, convert the energy released to useful form, namely electricity.

The requirement for high temperatures to achieve fusion is unavoidable; the choice of operating fuel density is open. For example, in a large reactor operating in steady state the fuel density would be quite low—about 1/100,000 of the density of the atmosphere—practically a vacuum. Even so the fusion power released per unit volume would be about 10 megawatts or more per cubic meter of reacting fuel. Higher fuel densities are possible; but since fusion power increases as the square of the fuel density, reactors working at much higher densities must necessarily operate in a pulsed mode, that is, with an intermittent combustion cycle, like an internal combustion engine. In any fusion reactor, however, the total amount of fuel present at any one time would only be a fraction of a milligram.

Confinement problem

Confinement of the hot fuel gas, that is isolating it from physical contact with the reactor cham­ ber walls, has always been the central problem. At first this problem seemed insolvable even in principle. Then it was realized that the high temperature necessary for fusion itself could help solve the problem. I am referring to the fact that at fusion temperatures matter exists only in the plasma state, ions and electrons, and that these can be controlled by magnetic fields. Since the earliest days of fusion research this has been the main approach: to use intense magnetic fields to control the plasma, in other words to attempt to confine it within a magnetic bottle.

As I implied in using the words “attempt to confine,” the stumbling block for fusion research in the past has been the failure of magnetic bottles to live up to expectations. This single circumstance dominated the research picture for many years. This is the circumstance that has now changed so radically.

To anticipate things I will later discuss, let me say that the present situation is that the origins of the past failures of magnetic confinement, namely plasma instabilities, are well understood, and that powerful and effective means for dealing with these instabilities have been devised and proved out in the laboratory. In fact, the recent optimism in the fusion community stems from the circumstance that the stabilization principles involved are being found to remain effective in plasmas whose properties are not far below those needed in a fusion reactor. Furthermore, new experiments are coming up that should push these limits even farther. The optimists among us—and I’m one of them—look on these new experiments as being the likely immediate predecessors of what might be called scientific feasibility demonstrations for fusion, that is, experiments in which the principles of magnetic confinement would be proved at reactor densities, temperatures and confinement times.

Before I launch into more details let me digress again and say a word about optimism and pessimism inside and outside the fusion community. Optimism has kept us going through some very black times. It has also in the past led to premature rejoicing as soon as a little light showed through the clouds. I guess this reaction is a little bit like that good feeling you get when you stop hitting your thumb with a hammer.

On the other hand, pessimism has little it can say about what are now solid scientific accomplishments in fusion research, nor even about the ultimate importance and value of achieving fusion power. Where the confrontation occurs, and where it will remain until fusion power is a reality, is at the question of the significance of new results as a valid guide to the future and on the timetable for translating these results into practical hardware.

Magnetic dilemma

Let me return to some basics about magnetic confinement. Charged particles immersed in a magnetic field must execute helical coil spring-like orbits in that field. If the field is sufficiently intense, the diameter of the helices will be small compared to that of the reactor chamber. When this is true, particles should only be able to reach the chamber walls in the transverse direction—that is, across the field lines—by step-by-step diffusion arising from collisions between the particles, the so-called classical rate of diffusion of plasma across a magnetic field. At fusion temperatures and in a straight tube this classical rate calculates to be orders of magnitude slower than that needed to satisfy fusion requirements. This result, namely, that a strong magnetic field in a straight tube, should effectively prevent the flow of particles across that field has been around for at least 30 years. It represents both the starting point and the reference standard for magnetic confinement.

To convert the basic idea into a useful plasma confinement system is another story. This kind of magnetic confinement is good for stopping transverse flow, but worthless in inhibiting flow along field lines. There are three ways to resolve this dilemma:

1. Make the tube so long that its open ends don’t matter, this means a kilometer or so at high density pulsed reactor conditions or hundreds of kilometers for a steady-state reactor —not a very attractive possibility.
2. Restrain the flow of plasma along the field lines—this is the mirror machine idea.
3. Or, and this one is the most popular choice for many reasons, return the field lines on them­ selves within a doughnut-shaped chamber, so that plasma particles can move freely along the lines without escaping.

The last two ways gave rise during the earliest days of fusion research to two simple, neat and intuitively obvious forms, the so-called open and closed magnetic bottles as shown in Figure 1. As I said, the open system is called a mirror machine since it works by trapping particles between magnetic mirrors (the mirrors are the strong field regions at the ends). The closed bottle is a primitive fore­ runner of the Stellarator idea that I will discuss later.

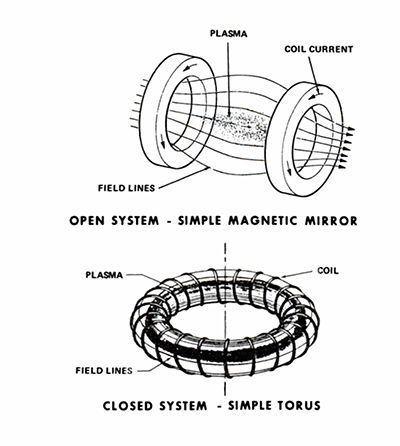
Like many simple and neat solutions to difficult problems these two are virtually worthless as originally proposed. Nevertheless they embody the basic confinement principles of later magnetic bottles that have proved to be effective.

Why did these first systems fail? They failed because they were subject to the simplest and most catastropic of all plasma instabilities, the magnetohydrodynamic (MHD) or hydromagnetic instability, in which the plasma moves as a whole across the confining field in the downhill direction on any average magnetic gradient that happens to be present. This kind of instability is like that of a ball perched on a hill; the ball is the plasma. Let it go and it rolls off the hill, here that means across the field. In the simple toroid the field weakens away from the central axis of symmetry at every point on every magnetic line; confinement is not possible and the plasma slides to the outer wall in microseconds. In the simple open system a similar catastrophe can happen, here it occurs sideways between the mirrors.

Stabilization principles

The first major success of fusion research—nailed down about a decade ago—was the suppression of MHD instabilities. This success was achieved in both open and closed systems by reshaping the confining fields. From this work emerged two basic principles of plasma stabilization now used in one form or another in almost every modern fusion experiment. These two principles are magnetic shear and the magnetic well.

Figure 2 shows the idea of magnetic shear. In a sheared field the lines are all helices, except for the one down the axis. But what’s important is that the helical pitch angle varies between successive layers of field lines, if you can think of layers of such things. This means the lines form a kind of multi-layered basket-weave pattern.

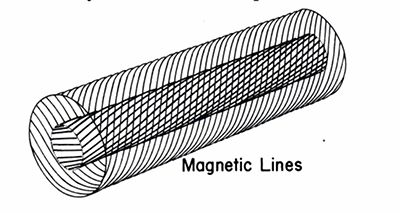
The helical nature of the field lines in a closed toroidal system with magnetic shear has two important consequences: First, all field lines—except the one in the middle of the tube, the magnetic axis—spiral as they go around the tube. Sometimes they are nearer to the outside wall, sometimes nearer to the inside wall. This effect is called rotational transform, and it was first used in the Stellarator. Its effect is to average out the “downhill magnetic gradient effect.” The second effect of sheared fields is that it can also inhibit other plasma instabilities (other than MHD) that could cause losses across the field. Shear in effect “shorts out” the localized unstable accumulation of charges by taking advantage of the high electrical conductivity of plasma along field lines.

Strong shear is one basic principle, the magnetic well is the other. Magnetic wells are made by shaping the magnetic field within and around a plasma so that the plasma sits at a point of relative minimum in the field. If this trick can be accomplished then it is “uphill” on the magnetic gradient no matter what direction the plasma tries to move. Therefore in deep magnetic wells, MHD instabilities are impossible.

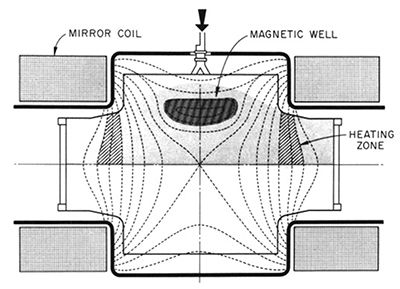
Magnetic well fields can be made either by modifying the field coils or by a combination of currents flowing in conductors outside the plasma, and currents induced in the plasma itself, or in conductors floated inside the plasma. Perhaps the best-known application of the magnetic well idea is the mirror machine. The first experimental test was carried out by M. S. Ioffe and his co-workers in Moscow in 1961. Figure 3 shows the general shape of the field lines and the confined plasma in a modern version of the magnetic well type of mirror machine as made by a “baseball coil”—one shaped like the seam on a baseball.

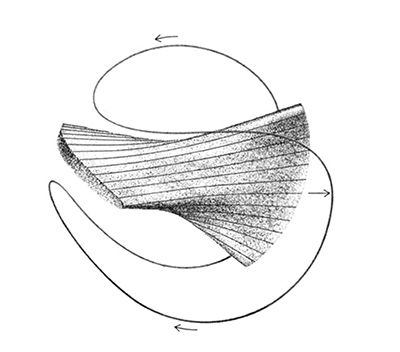
Suppressing MHD modes does not end the instability story, however. When they are gone some less violent but still worrisome modes may remain. Even though these modes cannot expel the plasma bodily, they can cause it to diffuse excessively rapidly across the field lines of a torus—or out the ends of a mirror machine. On a time scale where MHD modes dump plasma in microseconds these weaker modes dissipate it in milliseconds. In all but very high density pulsed systems millisecond confinement is too short. In a steady-state reactor, tenths of seconds to a second or so would be required.

The modes I am now discussing are describable as plasma turbulences, involving laser-like wave amplification effects that lead to unstable plasma oscillations. They are the last hurdle before scientific feasibility, and it is in their control that major recent progress has been made.

The bad effects of turbulence modes were probably first noticed in closed systems. There the experiments strongly suggested a fundamental limitation on confinement, proposed by David Bohm about 30 years ago to explain some peculiar effects in gas discharges in magnetic fields. According to this dismal law (dismal for fusion, that is), magnetic confinement should get progressively worse with increasing plasma temperature, rather than getting better as in classical diffusion. Not only that, but it was predicted to vary only as the first power of the magnetic field, rather than improving as the square in classical diffusion. Thus high magnetic fields would be of little help. For years experimental evidence in toroidal systems seemed to support the Bohm Law. This law was found to hold in the Princeton Model C Stellarator, at that time (circa 1966) the largest and most powerful toroidal experiment in the world.

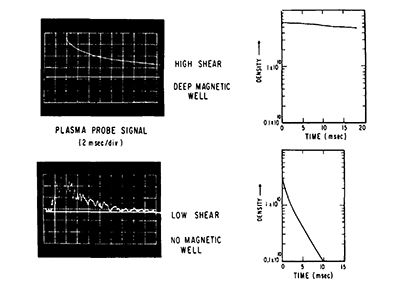
Faced with the fact of Bohm diffusion, the fusion community went back to the drawing board. Probably the first ray of light came when magnetic wells were tested in toroidal geometry. Special experiments were set up in which ring conductors inside the plasma chamber were used to shape the field. Though no one thinks of these suspended ring experiments as leading to reactors, they provide critical tests of stabilization principles in closed confinement systems. A clear-cut example of plasma stabilization in such a torus is provided by the Princeton Spherator experiment, where both shear and magnetic well depth can be varied.

Figure 4 shows the stabilization achieved. The upper scope traces and density curve show stable confinement; the lower ones show turbulence and loss of confinement.

There is another important aspect of fusion plasma confinement that I have not mentioned. It has to do with the beta value of a fusion plasma. Beta measures the energy density of the plasma, as compared to the energy density of the confining field. When beta is small the plasma hardly perturbs the magnetic field by its presence; when it is large it may markedly weaken it. Beta equals one is the limit; there the plasma has pushed out the field entirely. The magnetic fields can hold no more. Beta is not too important in academic studies of confinement. However, it is very important in a reactor since it measures how effectively the magnetic field is being used—therefore it involves dollars since magnetic fields cost money. Since fusion power varies as beta squared, high beta is desirable from an economic standpoint.

Experiments have now been performed that exhibit both high beta and classical diffusion in a tubular plasma. These experiments are called theta pinches, since they work by magnetically squeezing the plasma with currents flowing in coils wound around it (in the theta direction). A striking example of a stable high beta plasma column is shown in Figure 5.

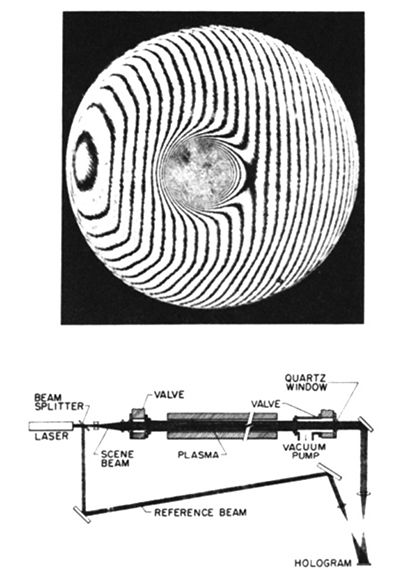
The device is the Los Alamos Scylla IV, and part (a) of the figure shows a laser interferometer picture of the compressed plasma. In a similar experiment in the United Kingdom, it was shown that such columns diffuse classically, not by the Bohm Law.

One very important additional aspect of high beta plasmas is that they can dig their own magnetic well. Thus they can actually help stabilize themselves, if you speak to them nicely. This idea is also implicit in the Astron experiment at our lab, where the well is to be dug with high energy particles.

A fine experimental example from Oak Ridge National Laboratory of both stable high beta con­ finement and self-dug magnetic wells is shown in Figure 6.

The upper half of Figure 6 shows contour lines of magnetic intensity as modified by mirror trapped high energy electrons. The lower half shows the magnetic field contours without plasma. The plasma electrons indeed have dug a well for themselves and are quite happy to stay there.

Let’s stop a minute and see where we are. Magnetic confinement, at first a wobbly and poorly understood business, has been refined to the point where it can be made to work. Is it good enough for fusion reactors?

First, let’s recognize that, with one exception, all of the experiments mentioned so far have been preparatory ones, that is, they were experiments conducted on nonfusion (that is, low density or low temperature) test plasmas. The exception was the theta pinch, where the plasma was both hot and very dense. Beyond that experiment what else is known about confining real fusion plasmas? Now I would like to discuss two more experiments, plus follow-ups, that have encouraged fusion researchers to feel in their bones that magnetic confinement really should work for fusion reactors.

The first of these is the Tokamak T-3 experiment in Moscow. A tokamak is a toroid in which magnetic shear and magnetic well effects are produced by a combination of the usual external fields with fields from a heavy induced electrical circulating current flowing in the plasma itself. In the T-3 experiment, plasma ion temperatures of about 10 million degrees were achieved, at close to reactor densities. The confinement time was about 10 milliseconds—a world’s record for that density and temperature. But what excited the fusion community most was the fact that the measured confinement time was within about a factor of three of the calculated classical lifetime in a torus, and was far above the Bohm value. The results achieved by the Soviets have since been confirmed at Princeton, and should soon be extended even further in new experiments.

The second experiment to come within shooting distance of classical confinement, in this case a mirror experiment, is the 2X experiment at the Lawrence Radiation Laboratory. In this experiment the plasma was hotter, nearly 100 million degrees; the density was the same. Here the classical time was not as long. Figure 7 shows a historical sequence of plasma confinement curves in 2X, showing the improvement in confinement caused by the progressive elimination of instabilities over the years, and the approach to classical confinement (top curve).

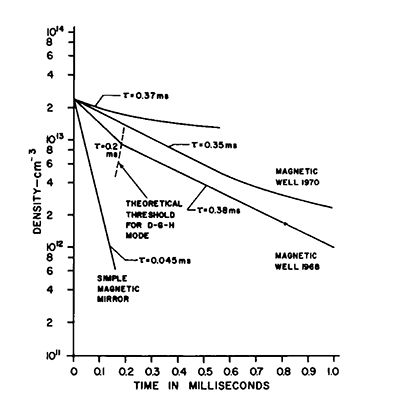
The third fusion plasma confinement result I have already mentioned—the Scyllac IV theta pinch at Los Alamos. These three experiments and their recent back-ups represent the visible basis for present optimism in fusion. Less visible but no less important is a massive accumulation of prior experiments and theory. While plasma theory is a very difficult business, there are more and more cases where theory and experiment agree closely, so that prediction based on theory is becoming much more of a science and less of an art.

There are many other new generation experiments in preparation in other laboratories around the world, including, we understand, some new and larger tokamaks in the USSR. Will these new generation experiments be successful? All of them? Any of them? We don’t know for sure.

Still, the recent encouraging data on fusion confinement is heady stuff. And you can’t blame those of us in fusion for beginning to think about reactor problems. One immediate question is: How good does confinement have to be for a reactor, and how close might we be to it? It is here that the toroidal systems really have the edge. The point is, in an MHDstable torus, particles can only escape by diffusion across the magnetic field. Since diffusion times vary as the square of the dimensions, you can always buy back confinement time in a somewhat nonclassical torus, just by scaling up the size a bit. Figure 8 illustrates this point.

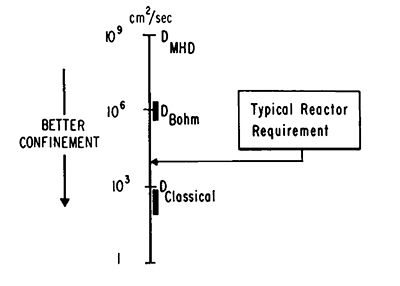
As can be seen, even a failure to achieve confinement by a factor of 10 or more would seemingly not be a worry. Of course we cannot assume before the fact that the present favorable trends will continue all the way to a reactor, but there are certainly strong reasons for hope.

Suppose we assume that we are indeed on track in at least one of the approaches to fusion. What then are the problems of engineering a fusion reactor, and what might it cost? The answer will of course depend on which system and on other details, but some things have turned up through studies. First, there do not appear to be major engineering problems—with some important exceptions—that have not already been faced in the fusion program, or in the space program or in the fission reactor program. By that I mean the problems of generating intense fields, of obtaining high vacua, of heat transfer and of other nuclear­related technology. The exceptions that come to mind have to do with the way the reactor plasma is to be heated, something not yet tested full-scale, and with radiation damage problems at the reactor chamber wall. But even these problems are not immutable. In some approaches, plasma heating should not be a major problem, and in others radiation damage effects should be minimal. The point is that fusion is not one thing. It represents a broad new approach to power generation with new flexibilities and new potentialities.

An example of new possibilities is direct conversion. Some fusion reactions, the best example being the deuterium-helium₃ reaction, release their energy as kinetic energy carried entirely by charged reaction products. Since electricity is the flow of charges, it should be possible to convert particle energy directly to electrical power. In principle the efficiency of this conversion could be very high, 90 percent or possibly more. At the Lawrence Radiation Laboratory we are investigating an idea for direct conversion that uses the end leakage out of the mirror machine. In recent small-scale tests we have proved out many of the principles involved and have achieved measured conversion efficiencies in excess of 80 percent. Just for fun, an artist’s concept was drawn of what a 1,000 megawatt direct converter attached to a mirror reactor might look like (see feature image at top of page and figure 9 below). One of the nice features of the system is that it would generate high-voltage direct current directly, and that its cost per kilowatt converted might be substantially lower than that of steam turbine-alternator conversion systems.

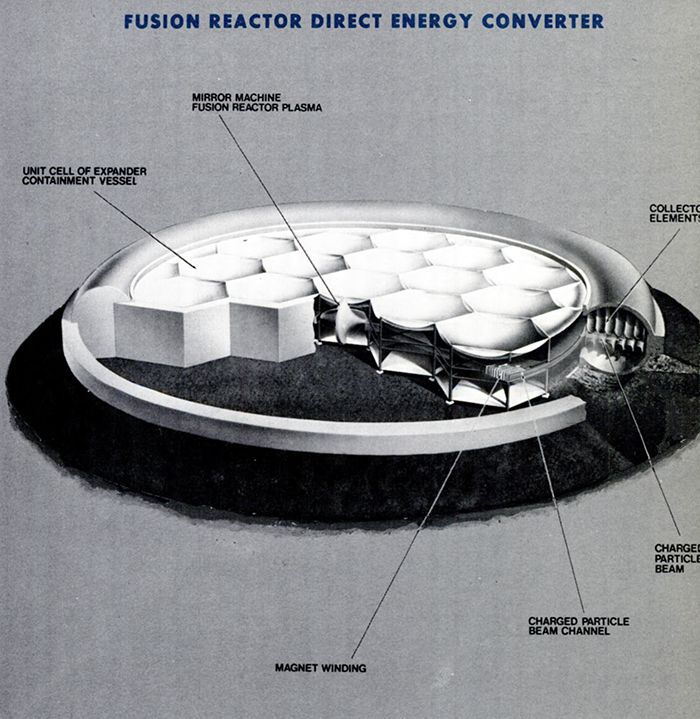
I would like to venture some predictions. These predictions will be those of an optimist, but I hope not those of a fool. I also hope I have made you aware of the fact that no decisive experiment has yet been performed proving conclusively that fusion is feasible, however encouraged we may be.

Figure 10 tries to trace the course of development of fusion power from the time deuterium was first discovered up to the present and into a possible future.

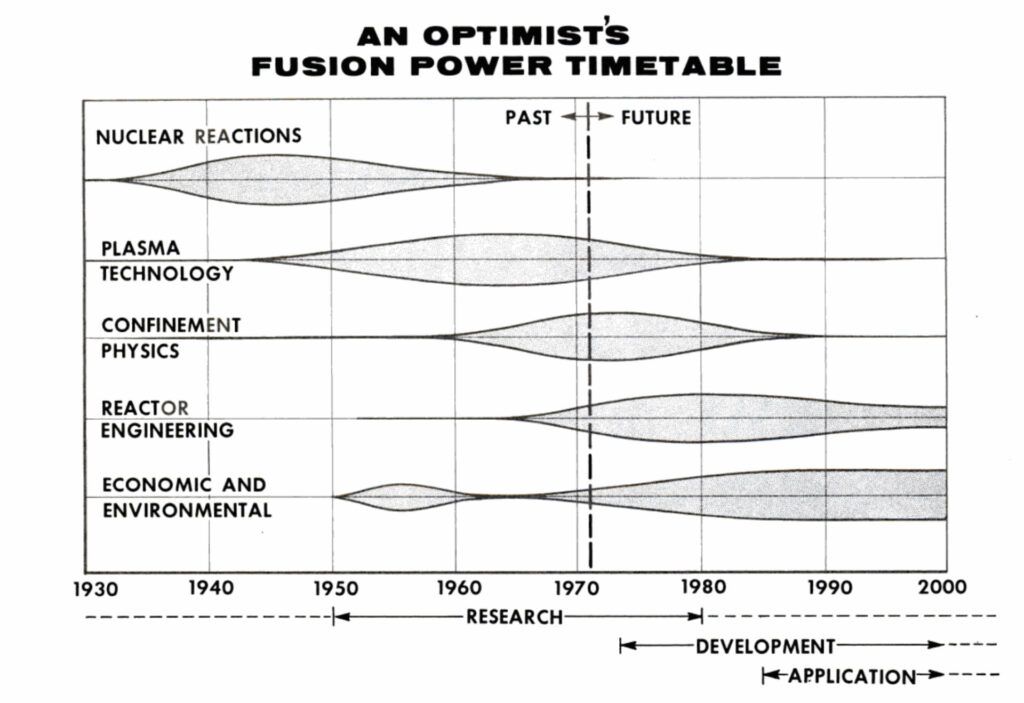
The width of the bands measures the effort or urgency level (within that category) as a function of time. As you see, I believe plasma technology is already in good shape. Confinement physics is soon to be over the hump and engineering should grow. At the bottom of the figure I show my idea of the overlapping sequences: Research and development, and practical application. By my timetable, first applications of fusion power could come in the 1980s and economic and environmental aspects should be in full swing by 1990. This all presumes that the critical next five years of confinement physics goes as shown. To make that happen, fusion research cannot exist under a static or declining budget, and to reach practical power on this timetable, engineering development must clearly grow.

As Tommy Thompson implied, fusion power is indeed an uncertain certainty. But I believe we have the clear and present opportunity to bring that desirable certainty much closer. There is really no reason to wait for our grandchildren to finish the job.